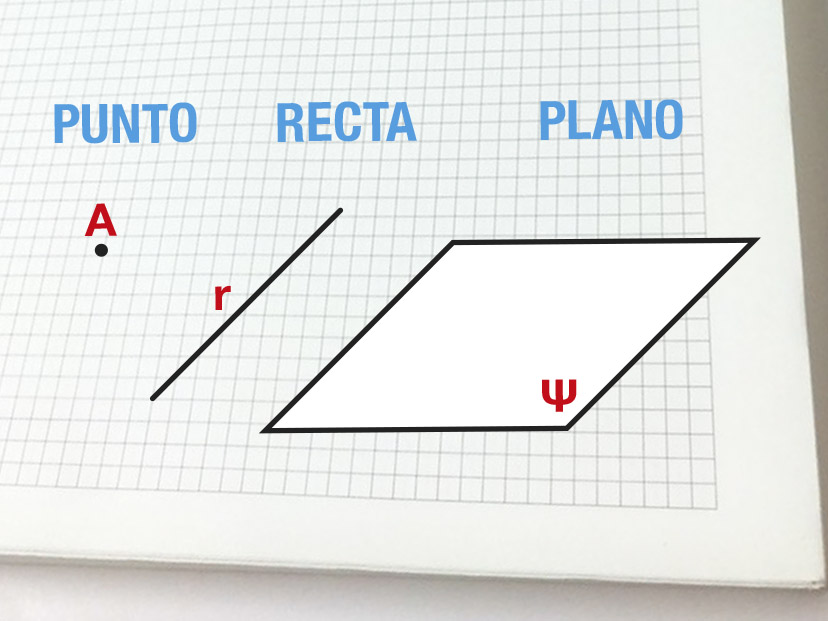
Punto, recta y plano son los tres conceptos clave y básicos de la geometría. Son la base sobre la que se empieza a trabajar y sobre ellos se construyen todos los demás conceptos geométricos que conocemos y que tienen gran aplicación en diversos campos.
- Punto: está formado por la intersección de dos rectas. Es una figura geométrica sin dimensión: no tiene largo, ancho ni volumen.
- Recta: está formada por un número infinito de puntos alineados. Tiene una sola dimensión (tiene largo pero no ancho).
- Plano: está formado por un número infinito de rectas y puntos. Tiene dos dimensiones (largo y ancho), pero no tiene volumen.
El punto
Queda establecido al cortarse dos líneas. Además, es una figura geométrica sin dimensión. ¿Qué quiere decir eso? Que no tiene longitud, área ni volumen. Sirve para establecer una posición en el espacio. A los puntos se los suele nombrar con letras mayúsculas.
Existen dos tipos de puntos:
- los colineales, que se encuentran en una misma recta
- los coplanarios, que están contenidos en un mismo plano.

La recta
Está formada por un número infinito de puntos alineados. Si conocemos la posición de dos puntos, podemos trazarla. Por eso es correcto afirmar que la recta queda determinada por dos de sus puntos, o que por dos puntos pasa una sola recta. A las rectas se las suele nombrar con letras minúsculas. Una recta contenida entre dos puntos se llama segmento. Para representar un segmento se escribe el nombre de los puntos (extremos) con un guión encima.
Existen tres tipos de rectas
- las rectas paralelas están situadas en el mismo plano y no tienen ningún punto en común. Claro, nunca llegan a cruzarse
- las rectas perpendiculares son aquellas que al cortarse forman 4 ángulos rectos
- las rectas oblicuas son aquellas que al cruzarse no forman ángulos rectos.

El plano
Es un elemento geométrico sin volumen y formado por un número infinito de rectas y puntos. También existen otras maneras de definirlo: a) tres puntos no alineados, o b) una recta y un punto exterior a ella. Si una recta divide a un plano obtenemos dos partes que llamamos semiplanos. Si necesitás comprobar si una superficie es plana o no, solo tenés que colocar una regla encima. Si esta toca todos sus puntos en cualquier dirección, podemos afirmar que la superficie es plana. Al plano se lo suele nombrar con una letra del alfabeto griego.