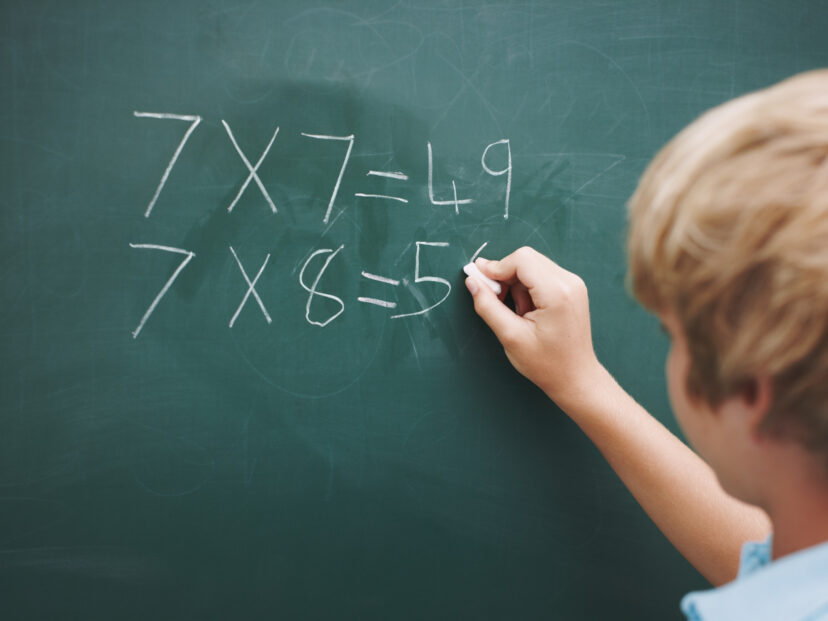Las tablas de multiplicar no son solo un ejercicio escolar; constituyen una herramienta esencial que usamos a diario, ya sea para hacer cálculos rápidos al hacer compras o para identificar patrones matemáticos en nuestro entorno.
Es probable que muchos de nosotros recordemos haber aprendido a multiplicar usando los dedos, con canciones o simplemente memorizando los resultados sin comprender su significado real.
Aprender las tablas de multiplicar es tan básico para el desarrollo posterior de las matemáticas que plantea una duda fundamental a profesores y familias: ¿cuál es el método más eficaz para dominar un conocimiento tan básico y esencial? Frente al tradicional aprendizaje de memoria, surgen alternativas para facilitar su aprendizaje y agilizar los cálculos.
Existen muchas formas de aprender a multiplicar, y una de ellas es usando los dedos de las manos, lo que facilita el razonamiento y la comprensión de los números de forma intuitiva. Sin embargo, durante años se han empleado métodos de enseñanza enfocados únicamente en la memorización, en lugar de promover una comprensión más profunda.
¿Cómo usar los dedos para multiplicar?
Esta técnica es especialmente útil para las tablas del 6 al 10. Primero, numeramos los dedos de ambas manos: asignamos el 6 a los meñiques, el 7 a los anulares, el 8 a los dedos medios, el 9 a los índices y el 10 a los pulgares.
Para multiplicar, por ejemplo, 6 x 7, unimos el meñique izquierdo (6) con el anular derecho (7). Contamos los dedos que están juntos y los que se encuentran debajo; en este caso, son 3 dedos, cada uno con un valor de 10, lo que nos da 30. Luego, multiplicamos los dedos restantes: 4 de la mano izquierda y 3 de la derecha, que resultan 12. Finalmente, sumamos ambos resultados y obtenemos 42.
También te puede interesar > ¿Sirve para algo aprender cosas "de memoria" en la escuela?
En otro ejemplo, 9 x 8, unimos el índice derecho (9) con dedo medio derecho (8). Contamos los dedos que están juntos y los que se encuentran debajo; en este caso, son 7 dedos, cada uno con un valor de 10, lo que nos da 70. Luego, multiplicamos los dedos restantes: 1 de la mano izquierda y 2 de la derecha, que resultan 2. Finalmente, sumamos ambos resultados y obtenemos 72.Vídeo de explicación.
Con este método se llevan a cabo, de forma implícita, múltiples actividades que fomentan el razonamiento. Por ejemplo, se multiplican las tablas del 1 al 5 y se suman los resultados para calcular las tablas del 6 al 10. Además, como aspecto adicional no relacionado directamente con las matemáticas, este sistema también ayuda a aprender el nombre de los dedos. Aunque podría parecer un detalle trivial, es importante destacar que algunas personas no los conocen.
Comprensión versus memorización en el aprendizaje de las tablas de multiplicar
Aunque muchos expertos consideran que memorizar las tablas de multiplicar es la mejor manera de aprenderlas, comprenderlas primero facilita el aprendizaje y hace que recordarlas sea más sencillo.
Cuando les damos un significado y encontramos patrones, el proceso se vuelve menos mecánico y más significativo. Por ejemplo, en la tabla del 9, los resultados muestran un patrón decreciente en las unidades, comenzando por el 9 y restando un número en cada paso (9, 18, 27, etc.).
En la tabla del 5, todos los resultados terminan en 5 o en 0, facilitando la predicción de los resultados sin memorizar cada uno.
Este enfoque también permite deducir otras relaciones, como en la tabla del 4, donde los resultados son siempre el doble de los de la tabla del 2, o en la del 10, que simplemente añade un cero al número que estamos multiplicando. Comprender estos patrones ayuda a los estudiantes a visualizar las tablas, reduciendo la necesidad de memorización y mejorando su habilidad para aplicarlas en situaciones prácticas.
Importancia de la flexibilidad mental en las tablas de multiplicar
La flexibilidad mental en las tablas de multiplicar es clave para desarrollar agilidad en el cálculo, lo que facilita resolver problemas y tomar decisiones rápidamente en muchas situaciones cotidianas. Este tipo de habilidad permite descomponer y reorganizar los números para hacer operaciones más complejas de forma intuitiva.
Por ejemplo, si queremos multiplicar 48 por 25, podemos dividir el cálculo en partes: multiplicamos 50 por 25, obteniendo 1250, y luego restamos el resultado de 2 por 25 (50), lo cual nos da 1200.
Otro ejemplo es cuando calculamos precios: si estamos comprando 15 artículos a 18 dólares cada uno, podemos multiplicar 15 por 20 (300) y restarle 30 (2 por 15, que son los dólares que hemos añadido para redondear), llegando así a un resultado rápido de 270 dólares.
Esta flexibilidad mental es útil al calcular propinas, ajustar presupuestos o dividir cantidades, permitiéndonos realizar cálculos precisos sin depender de calculadoras.
Beneficios a largo plazo y relaciones entre números
En conclusión, aprender las tablas de multiplicar a través de la memorización puede resultar útil para realizar operaciones simples de forma ágil, ya que permite responder rápidamente sin necesidad de pensar detenidamente. No obstante, adoptar un enfoque más reflexivo y flexible en el aprendizaje de estas tablas proporciona beneficios a largo plazo, ya que ayuda a entender mejor las relaciones entre los números.
Una manera efectiva de combinar ambos métodos es utilizar prácticas como juegos de matemáticas y ejercicios interactivos que estimulen tanto la memoria como la comprensión conceptual.
Por ejemplo, visualizar grupos de objetos puede facilitar la comprensión de la multiplicación como una suma repetida. Además, integrar desafíos y aplicaciones prácticas en la vida diaria, como calcular precios en una tienda o compartir cantidades de alimentos, puede hacer que el aprendizaje sea más significativo y relevante. Así, no solo se memoriza, sino que también se desarrolla un pensamiento matemático sólido que resulta fundamental para abordar cálculos más complejos en el futuro.
(c) The Conversation / César Eduardo Aceves Aldrete y Norma Edith Cortés González (Universidad de Guadalajara) / imagen: 123RF