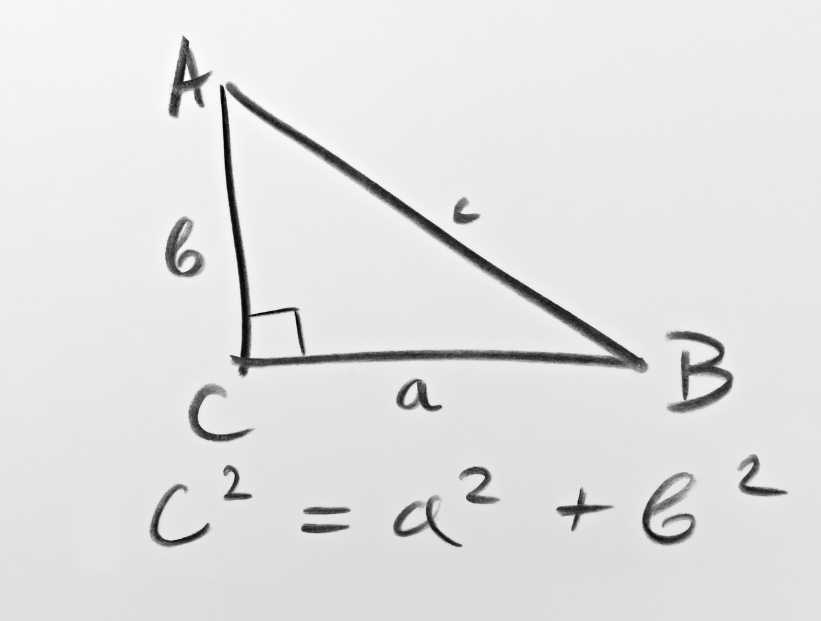
El Teorema de Pitágoras establece que en todo triángulo rectángulo se cumple que la suma de los cuadrados de las longitudes de sus catetos es igual al cuadrado de la longitud de su hipotenusa.

Si se nombra a los lados del triángulo como a, b y c, la fórmula que expresa esta teoría sería: a2 + b2 = c2. De aquí se desprenden otras cuentas que sirven para resolver problemas matemáticos.

Se dice que  fue comprobado en el siglo VI antes de Cristo (a. C). por el filósofo y matemático griego, Pitágoras, aunque podría haber sucedido en otro momento de la historia. Recientemente, aparecieron pruebas que parecen demostrar que no fue Pitágoras quien descubrió esta propiedad.

¿Desde cuándo se conoce el Teorema de Pitágoras?

Científicos de la Universidad de Rutgers, a cargo del doctor Bruce Ratner, analizaron una tablilla que data de 3.500 años atrás, que parece demostrar que el conocido como Teorema de Pitágoras fue desarrollado alrededor de 1.000 años antes del nacimiento del matemático al que se le atribuye el crédito.

También te puede interesar > ¡Eureka!: ¿por qué se grita eso cuando descubrimos algo importante?

Ratner analizó los gráficos que aparecen en la tablilla teniendo en cuenta la forma en la que los antiguos babilonios hacían las cuentas. Así determinó que este pueblo sabía cómo calcular la raíz cuadrada de un número.

También te puede interesar > Razonamiento espacial: ¿Por qué no vemos las vías del tren en paralelo?

Para lograr entender el razonamiento detrás de las líneas y números que aparecen en el objeto denominado como YBC 7289, tuvo que utilizar el sistema de conteo sexagesimal con base 60 que era utilizado por aquella antigua civilización.

La tablilla es un bloque de arcilla que fue hallado en el sur de la región Mesopotámica. Actualmente, está guardada en la Universidad de Yale, en Estados Unidos.